基础算法（一）

快速排序

快排

题目链接：785. 快速排序 - AcWing题库

快排的主要思想是基于分治

找到分界点

对于一整串数组，首先找到一个值作为分界点。分界点的取值有三种取值方法：

• 取区间的左边界
• 取区间的中间位置的值
• 随机取一个位置

调整区间

让分界点（设为x）前面的区间部分全都是小于等于x的值，数组后面的部分则都是大于等于x的部分。

递归处理左右两段

再对区间的左和右分别进行排序，只要两侧都成功排序那么整个区间就完成了排序。

---

该问题在处理的过程中主要的操作就是调整区间。并且最后的效果是让区间处于了两种互斥的不同状态。因此可以用双指针的做法，同时从前和末端向中间进行扫描，当他们一方扫描到需要进行交换的异端分子的时候，就等待另一端也扫描出同样的异端分子。当双方都扫描到对方的异端分子的时候，只需要将这两个异端分子同时交换，当两个指针相遇的时候，也就是处理好了所有异端分子的时候。

模板实现：

void quick_sort(int q[], int l, int r) {
  if (l >= r)
    return;
  int x = q[(l + r) / 2], i = l - 1, j = r + 1;
  while (i < j) {
    do
      i++;
    while (q[i] < x);
    do
      j--;
    while (q[j] > x);
    if (i < j)
      swap(q[i], q[j]);
  }
  quick_sort(q, l, j), quick_sort(q, j + 1, r);
}

第k个数

题目链接：786. 第k个数 - AcWing题库

找到分界点、选取区间

分界点的选取和快排相同。不同的是由于我们这里只需要第k小的数，因此在此时对划分出来的区间长度进行判断。如果k的大小小于左区间长度l，那么说明k在左区间，继续从左区间寻找第k小的数。如果k的大小大于l，说明k在右区间，在右区间寻找第(k - l)小的数。

---

代码实现：

int k_sort(int l, int r, int k) {
  if (l >= r)
    return q[l];
  int x = q[(l + r) >> 1], i = l - 1, j = r + 1;
  while (i < j) {
    do
      i++;
    while (q[i] < x);
    do
      j--;
    while (q[j] > x);
    if (i < j)
      swap(q[i], q[j]);
  }

  int sl = j - l + 1;
  if (k <= sl)
    return k_sort(l, j, k);
  else
    return k_sort(j + 1, r, k - sl);
}

归并排序

题目链接：787. 归并排序 - AcWing题库

1. 确定分界点：mid = (l + r) / 2
2. 分别递归排序左区间和右区间
3. 将两个数组合并

双指针合并

归并排序的主要思路就是将原本一个大数组，使用分治的思想，从单个数字的小数组进行不断的归并，最后获得的就是一个有序的新数组。因此主要的操作也就是在合并的这个操作上。

我们需要合并的数组有两个，因此这部分只需要用两个数组分别指向这两个数组的开头。然后再创建一个临时数组用于存放归并的结果。归并的过程中只需要每次都将两个指针中最小的那个输入加入临时数组中，然后将存入的指针后移，直到两个数组中其中一个被归并完毕，再将另外一个数组后面所有的结果合入答案的临时数组，最后将临时数组的结果写入原数组中即可。

---

模板实现：

void merge_sort(int q[], int l, int r) {
  if (l >= r)
    return;
  // 将区间分成左右两边，归并合并
  int mid = (l + r) >> 1;
  merge_sort(q, l, mid), merge_sort(q, mid + 1, r);
  int merged = 0, i = l, j = mid + 1;
  // 使用一个tmp的临时数组来存储归并后的结果
  while (i <= mid && j <= r) {
    if (q[i] <= q[j]) {
      tmp[merged++] = q[i++];
    } else {
      tmp[merged++] = q[j++];
    }
  }
  // 将多余结尾的部分插入tmp当中
  while (i <= mid) {
    tmp[merged++] = q[i++];
  }
  while (j <= r) {
    tmp[merged++] = q[j++];
  }
  // 将tmp合并好的数组返回输入给q[]中
  for (i = l, j = 0; i <= r; i++, j++) {
    q[i] = tmp[j];
  }
}

求逆序对的数量

题目链接：788. 逆序对的数量 - AcWing题库

逆序对：5 2 2 1 4，只要前面一个数比后面一个数字大，即为一个逆序对，因此有[5, 2], [5, 2], [2, 1], [5, 1], [5, 4]。这五个逆序对

首先，这个问题可以在对一个区间对半切割以后分为三种情况

• 在左区间中存在两个数字是逆序对
• 在右区间中存在两个数字是逆序对
• 在中间的两个黄色中，左区间存在一个数字是右区间的逆序对

其次，在这里引入归并排序的思想。在归并排序中，对于整个区间的排序本质上是对于最小区间（两个数字）之间的大小比较和扶正，最后扩展为整个区间的大小比较和扶正（分治）。带入到这个问题中，其实就是首先视 第三种情况 为最小的情况，然后最后的所有结果其实都是第三种情况的总和，所谓的第一种情况和第二种情况将会在最小区间的过程中被直接统计进入结果当中，也就是说我们只需要求出所有第三种情况逆序对的数量再加起来就是最后答案。

对于左右区间逆序对数量的判断

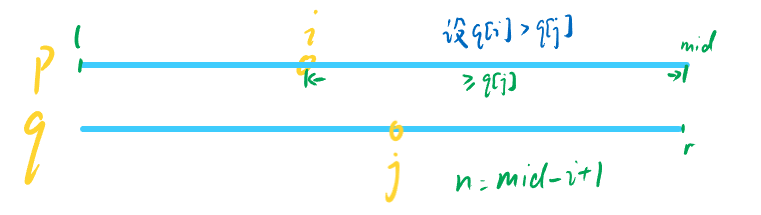
目前我们只考虑黄色的情况，因此对于一个区间，我们可以分成p和q两个部分来考虑。假设在p和q上有符合归并排序的两个指针i和j,且当前的情况符合了逆序对的p[i] > q[j]的定义。此时我们可以很容易就知道从i到mid这整个区间的数字都是大于q[j]的，而这个区间内数字的数量为mid - i + 1。通过这个规律，我们就可以知道如果我们想要统计所有的黄色情况中逆序对的数量，我们只需要将所有符合p[i] > q[j]情况的mid - i + 1数量加起来，就是最后答案。

---

代码实现：

关于计算逆序对的数量问题，假设总共有n个数据，由于每两个数据是一组，从n和n-1可以为一组的情况下来考虑，最后总共可以有(n(n - 1))/2大小的答案，如果数据集到达了类似100000量级的时候，最后答案会超过int的范围，因此有可能需要使用long long

const int N = 100010;
int tmp[N], q[N], n;

long long count_pair(int l, int r) {
  if (l >= r)
    return 0;
  int mid = (l + r) >> 1;
  // 将左区间和右区间分治的结果加起来
  long long res = merge_sort(l, mid) + merge_sort(mid + 1, r);
  int merged = 0, i = l, j = mid + 1;
  while (i <= mid && j <= r) {
    if (q[i] <= q[j]) {
      // 不符合逆序对，直接归并
      tmp[merged++] = q[i++];
    } else {
      // 符合逆序对的定义，归并的同时统计结果数量
      tmp[merged++] = q[j++];
      res += mid - i + 1;
    }
  }
  // 将归并以后长的部分合并
  while (i <= mid) {
    tmp[merged++] = q[i++];
  }
  while (j <= r) {
    tmp[merged++] = q[j++];
  }
  // 将排序以后的数组恢复到q[]内
  for (i = l, j = 0; i <= r; i++, j++) {
    q[i] = tmp[j];
  }
  return res;
}

二分

二分算法的本质为在一个区间中，存在一个位置使得区间的性质发生了变化，进而来寻找这个变化的点。

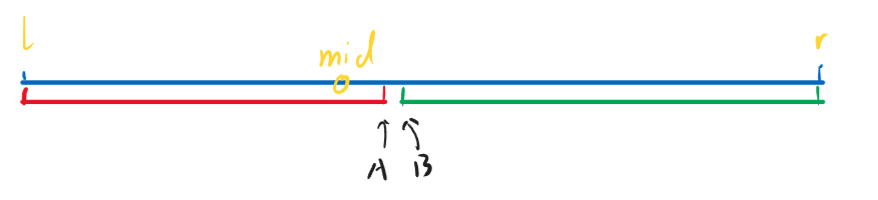
以上面这个图为例，对于红色区间和绿色区间，假设他们有不同的性质，且一个以A作为分界点，一个以B作为分界点。那么在使用二分的时候就有两种考虑

二分的分类讨论

在分类之前，首先对于所有的二分情况都有一个check()函数，用于判断某个点是否符合某个状态。在这里我们假设为某个点是否符合某个颜色（红/绿）区间的范围内

红色区间

区间左边界右移

如果我们需要使用二分法来取得A点的位置，那么假设我们先设了中点mid=(l + r)/2，那么就有两种情况。第一种情况是mid处于红色范围内，那么我们便很容易可以知道点A一定在mid到r之间

此时我们只需要有新的l = mid，然后从l到r中再次进行二分，直到l和r不为l < r的关系即可

区间右边界左移

和上图相反，如果我们是mid处于了绿色范围中，那么我们首先可以知道的是，mid这个点自身是不符合红色区间的范围的。因此我们也只需要有新的r = mid - 1即可。

---

模板实现：

int bsearch_left(int l, int r) {
  while (l < r) {
    // 由于r是以mid - 1来进行更新移动，因此如果没有+ 1的话将会出现死循环
    int mid = (l + r + 1) >> 1;
    if (check(mid)) {
      l = mid;
    } else {
      r = mid - 1;
    }
  }
  return l;
}

绿色区间

绿色区间和红色区间主要思路完全相同，只有区间在移动边界的时候条件不同。当需要右移区间的时候，有l = mid + 1，而区间如果要左移，只需要r = mid即可。因为这里这里不存在mid当区间长度为2的时候，如果右移区间会死循环的问题，因此mid直接取(l + r) >> 1即可。

---

模板实现：

int binary_search(int l, int r) {
  while (l < r) {
    int mid = (l + r) >> 1;
    if (check(mid)) {
      r = mid;
    } else {
      l = mid + 1;
    }
  }
  return l;
}

数的范围

题目链接：789. 数的范围 - AcWing题库

首先对于二分的题目，首先找出区分***红色区间***和***绿色区间*的check()函数。在这个题目中，主要目的是找到针对某个数字target，求出在数组中target最小的区间边界和最大的区间边界。因此可以通过大于等于target和小于等于target**来写出两个二分的函数，分别用于寻找左边界和右边界的位置

---

代码实现：

// 获取区间左边界
int bsearch_left(int l, int r, int value) {
  while (l < r) {
    int mid = (l + r) >> 1;
    if (numbers[mid] >= value) {
      r = mid;
    } else {
      l = mid + 1;
    }
  }
  return l;
}

// 获取区间右边界
int bsearch_right(int l, int r, int value) {
  while (l < r) {
    int mid = (l + r + 1) >> 1;
    if (numbers[mid] <= value) {
      l = mid;
    } else {
      r = mid - 1;
    }
  }
  return l;
}

高精度问题

高精度加法

题目链接：791. 高精度加法 - AcWing题库

高精度加法本质就是以字符串将数字读入以后，代码模拟手动计算十进制的过程，大于十就进一位。

---

模板实现：

这里一定要注意A[i]或者B[i]是否为数字，如果是字符的话还需要进行- '0'来让结果变成数字

vector<int> add(const vector<int> &A, const vector<int> &B) {
  vector<int> C;
  int t = 0; // 是否进位
  for (int i = 0; i < A.size() || i < B.size(); i++) {
    if (i < A.size())
      t += A[i]; // 记得确保这里加入的是数字，而不是字符
    if (i < B.size())
      t += B[i];
    C.push_back(t % 10);
    t /= 10;
  }
  if (t)
    C.push_back(1);
  return C;
}

高精度减法

题目链接：792. 高精度减法 - AcWing题库

高精度减法在实现之前，首先要确定被减项比减去的值要大，如果小的话则要提前分类讨论输出一个负号。

---

判断大小的一个简单实现：

bool operator>(const vector<int> &rhs, const vector<int> &lhs) {
  // 如果是"987"，读入的则是"789"。所以只需要从后向前逐步判断
  if (rhs.size() != lhs.size())
    return rhs.size() > lhs.size();
  for (int i = rhs.size() - 1; i >= 0; i--) {
    if (rhs[i] != lhs[i]) {
      return rhs[i] > lhs[i];
    }
  }
  return false;
}

---

对于减法的模拟流程，和加法主要的不同就是借位的操作。借位主要体现在计算第i位的A[i]和B[i]的运算的时候，如果有A[i] - B[i]结果是负数的话，那么A[i]就需要向A[i + 1]进行借位。这个时候我们只需要单独使用一个变量t，如果当前运算结果为负数需要借位了则让t为1，并且在每次运算前让A[i]减去t来实现借位的操作。

同时在执行完了减法的逻辑之后，由于减法和加法不同，可能会出现"0001"这种数字，我们还需要将所有除了最后一位（因为答案可能为"0"）的所有0给去掉。因为通过vector存储的数字是倒序，也就是说"0001"在数组里面是[1, 0, 0, 0]。因此我们只需要每次都把答案的末尾给剔除即可。

模板实现：

vector<int> sub(const vector<int> &A, const vector<int> &B) {
  // 执行函数前需要先确保传入的A比B大
  vector<int> ans;
  // 减法的流程
  for (int i = 0, t = 0; i < A.size(); i++) {
    // 判断之前是否进行了借位操作，然后将A[i]的值给t
    t = A[i] - t;
    if (i < B.size())
      // 使用借位以后的A[i]减去B[i]
      t -= B[i];
    // (t + 10) % 10 让答案处于0-9绝对值的状态
    ans.push_back((t + 10) % 10);
    // 如果相减以后的数字是负数代表需要在下一次操作进行借位
    if (t < 0) {
      t = 1;
    } else {
      t = 0;
    }
  }
  // 去掉多余的0
  while (ans.size() > 1 && ans.back() == 0)
    ans.pop_back();
  return ans;
}

高精度乘法

题目链接：793. 高精度乘法 - AcWing题库

高精度乘法的主要思路和高精度加法差不多，这类题目通常为一个大整数乘以一个小整数。对于这种情况下的乘法，我们只需要先将大整数和之前一样序列化成一个vector<int>的变量，然后和加法一样让容器每一位都和小整数相乘，大于10的部分留给下一位用于进位即可。

---

模板实现：

vector<int> mul(const vector<int> &A, int b) {
  // 如果为0的话，最后答案可能会为"00000"这种需要删除多余字符的vector
  if (b == 0) {
    return {0};
  }
  vector<int> ans;
  for (int i = 0, t = 0; i < A.size() || t; i++) {
    if (i < A.size())
      t += A[i] * b;
    ans.push_back(t % 10);
    t /= 10;
  }
  return ans;
}

高精度除法

题目链接：794. 高精度除法 - AcWing题库

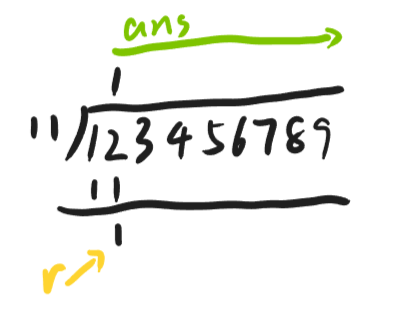
高精度除法的题目一般形式为一个大数除以一个小数。此时假设大数是123456789，小数是11。这种情况下按照正常计算逻辑大致如下：

由于在加减乘法中，我们都是将数字以[9, 8, 7, 6, 5, 4, 3, 2, 1]的顺序存储的，因此我们在计算除法的时候需要从A[A.size() - 1]的位置开始正常除法的计算逻辑，直到A[0]。其中在每次除的过程中，假设经过上次运算（默认的r = 0）的r是r'，那么在下一次计算的时候用于计算的余数则是r = r' + A[i]，然后只需要将除数放入ans的数组中，然后余数继续留给下一次计算即可。

---

模板实现：

vector<int> div(const vector<int> &A, int diver, int &reminder) {
  vector<int> ans;
  reminder = 0;
  for (int i = A.size() - 1; i >= 0; i--) {
    reminder = reminder * 10 + A[i];
    ans.push_back(reminder / diver);
    reminder = reminder % diver;
  }
  // 由于除法是正常顺序进行计算，因此需要将答案反转以后去掉前导0
  reverse(ans.begin(), ans.end());
  while (ans.size() > 1 && ans.back() == 0) {
    ans.pop_back();
  }
  return ans;
}